【人気ダウンロード!】 lim x → 0 1/x^2 246195-Lim x → 0 1/x^2 - cotx
Lim (1/x, x>0) WolframAlpha Area of a circle?
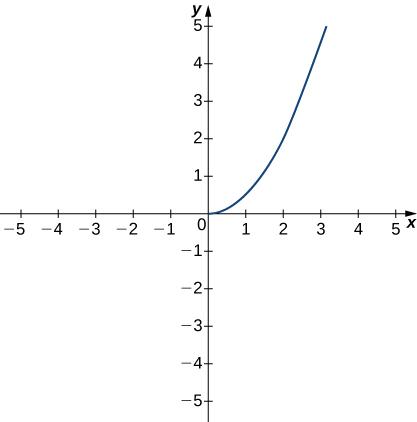
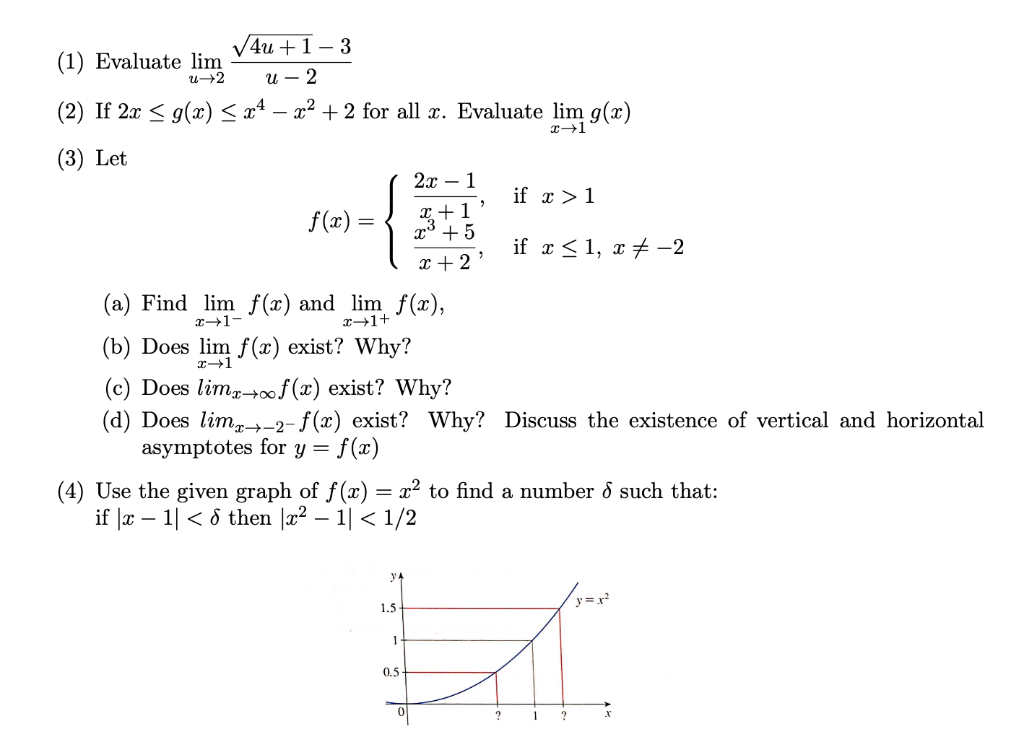
Lim x → 0 1/x^2 - cotx-L = lim x→0 (−1/4)(1 x)−3/2 2 = (−1/4) 2 We conclude that L = − 1 8 C L'Hˆopital's rule for indeterminate limits 0 0 Remark L'Hopital's rule applies to indeterminate limits only Example Evaluate L = lim x→0 1 − cos(x) x x2 Solution The limit is indeterminate 0 0 L'Hopital's rule implies, L = lim x→0 1 −Take the limit of each term Tap for more steps Split the limit using the Sum of Limits Rule on the limit as x x approaches 0 0 lim x → 0 x 2 − lim x → 0 x lim x → 0 x lim x → 0 x 2 lim x → 0 x lim x → 0 x Move the exponent 2 2 from x 2 x 2 outside the limit using the Limits Power Rule
Lim x → 0 1/x^2 - cotxのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 | 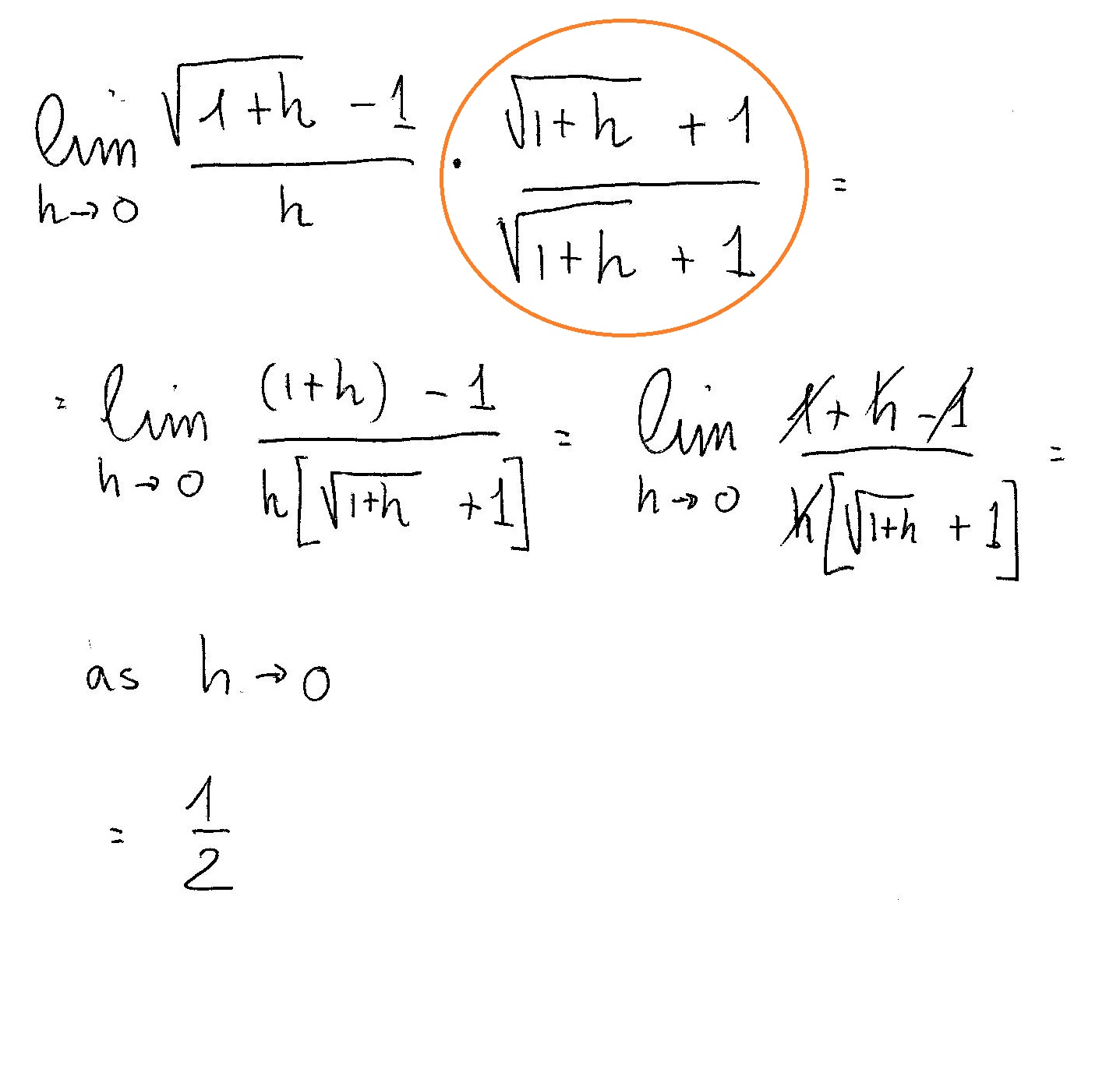 | |
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
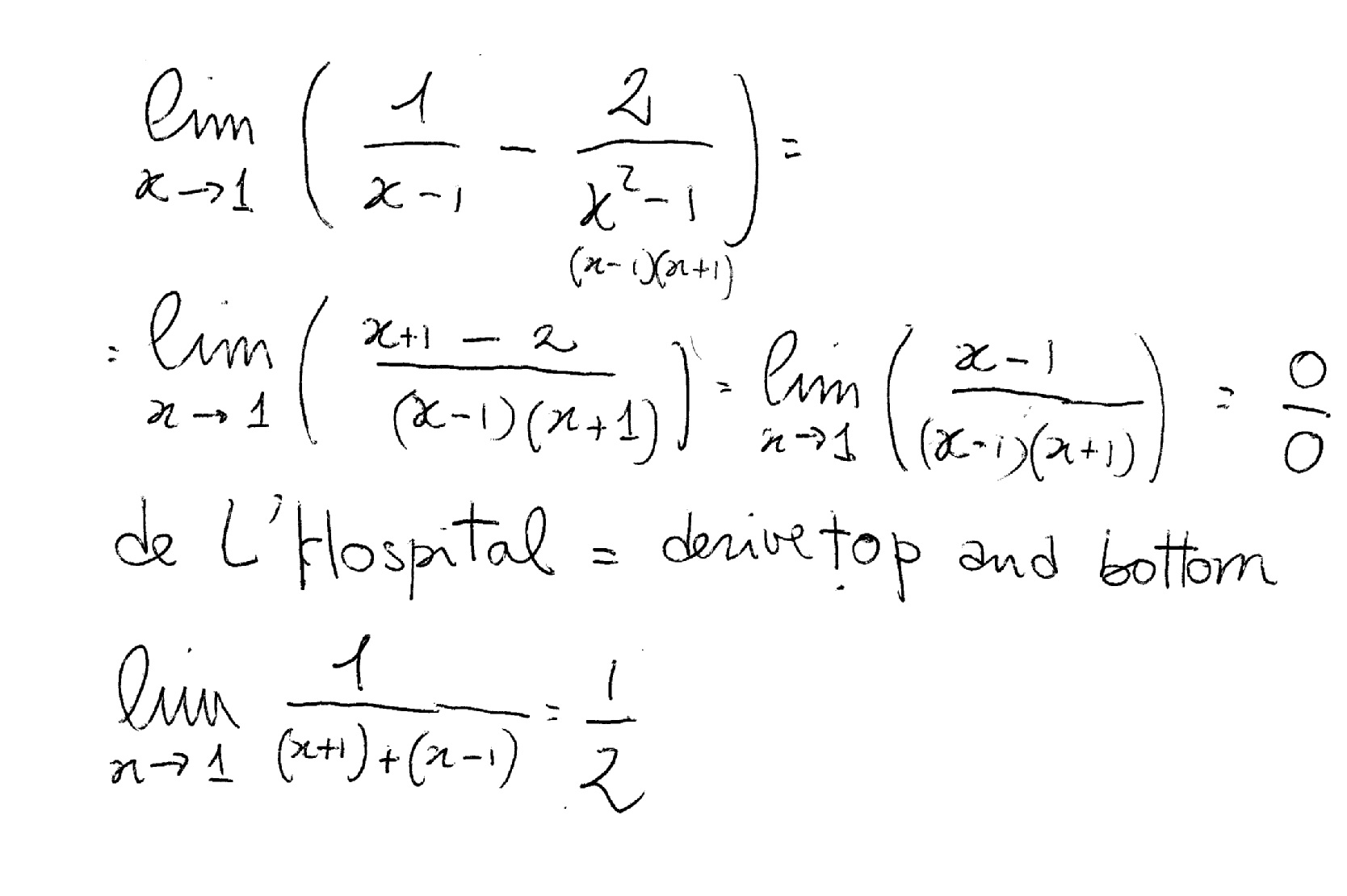 | 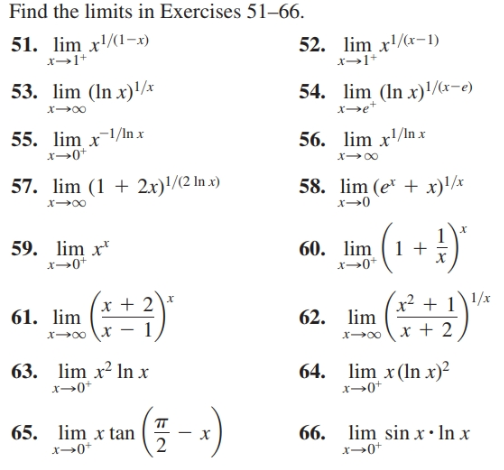 |  |
 |  | |
 |  |  |
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
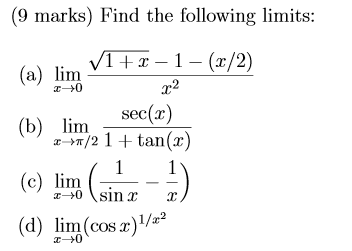 |  | |
 | 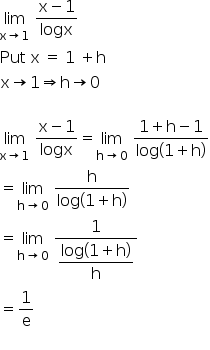 | |
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 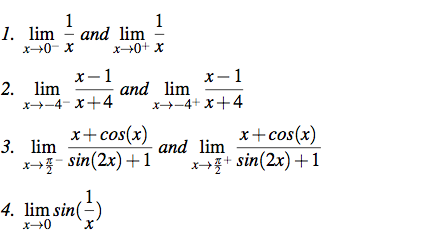 |  |
 |  |  |
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | 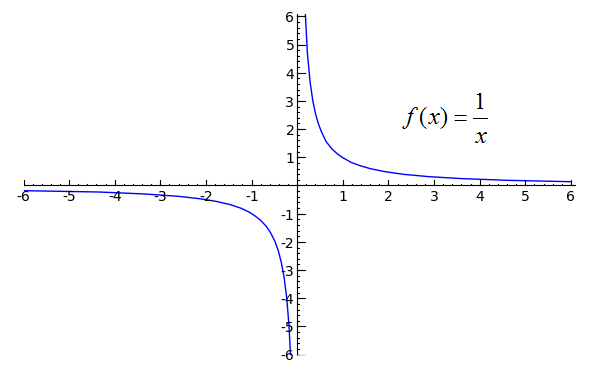 |
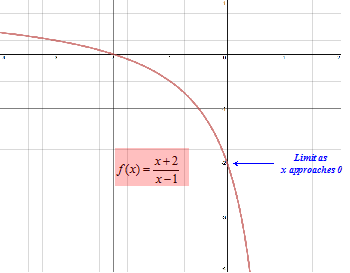 |  |  |
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 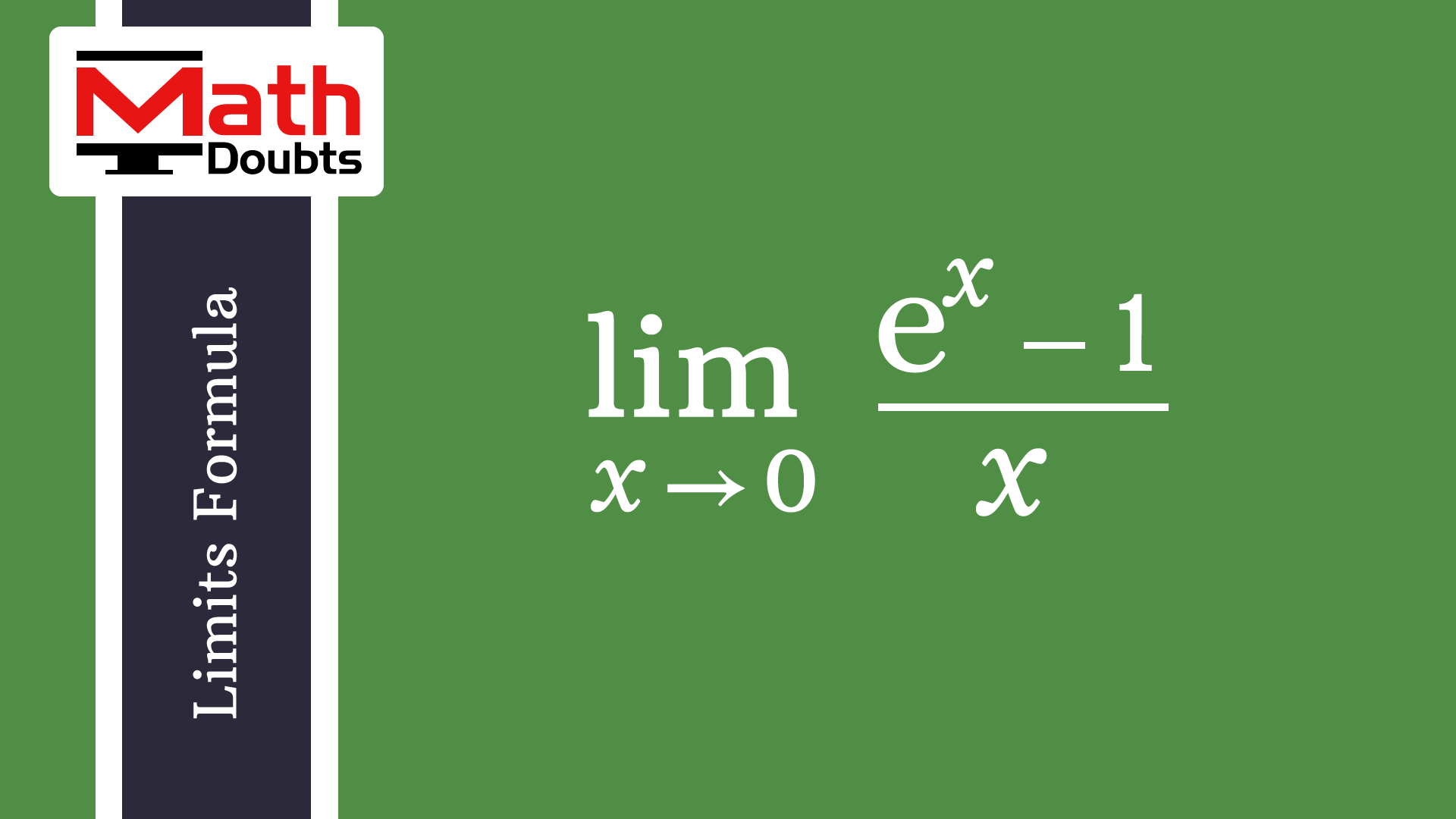 |  |
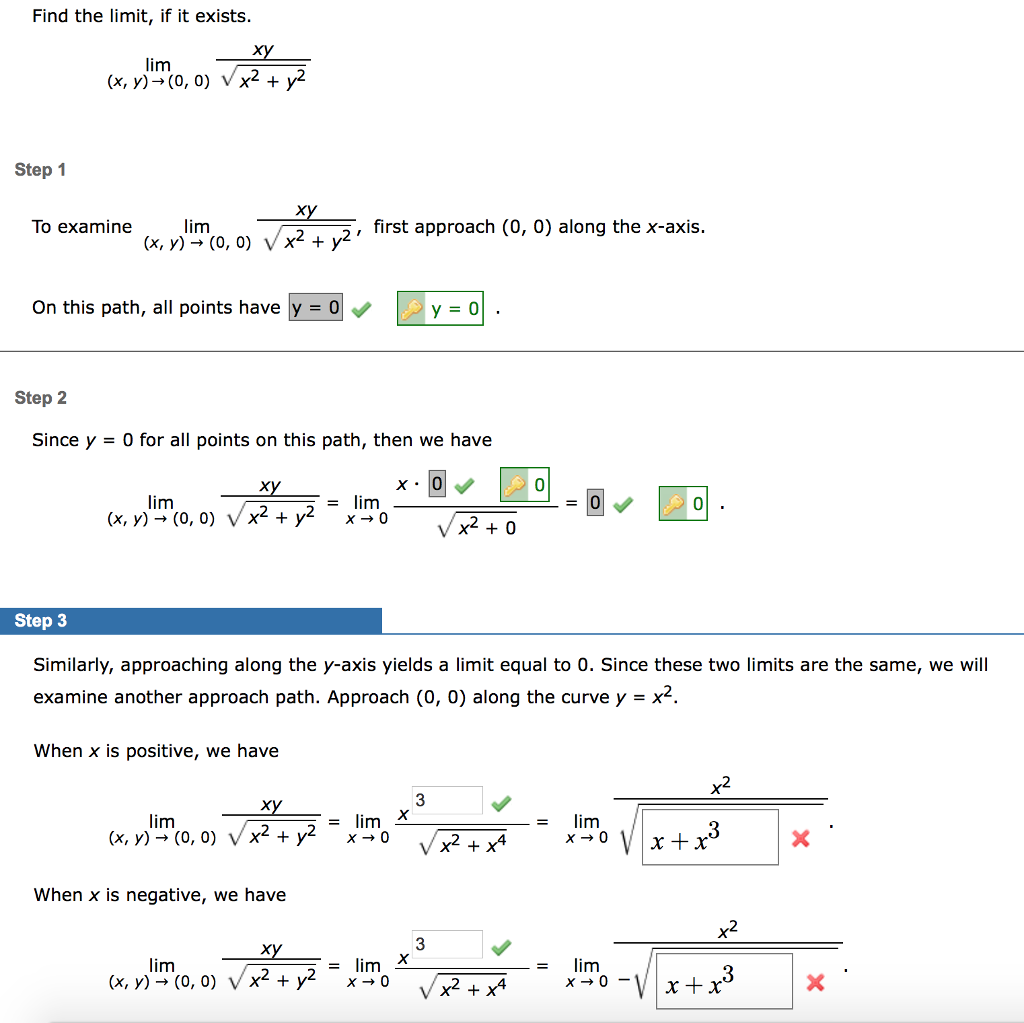 |  |  |
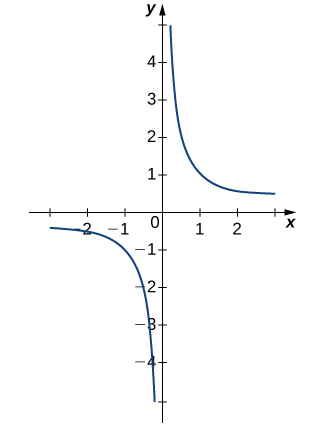 |  |  |
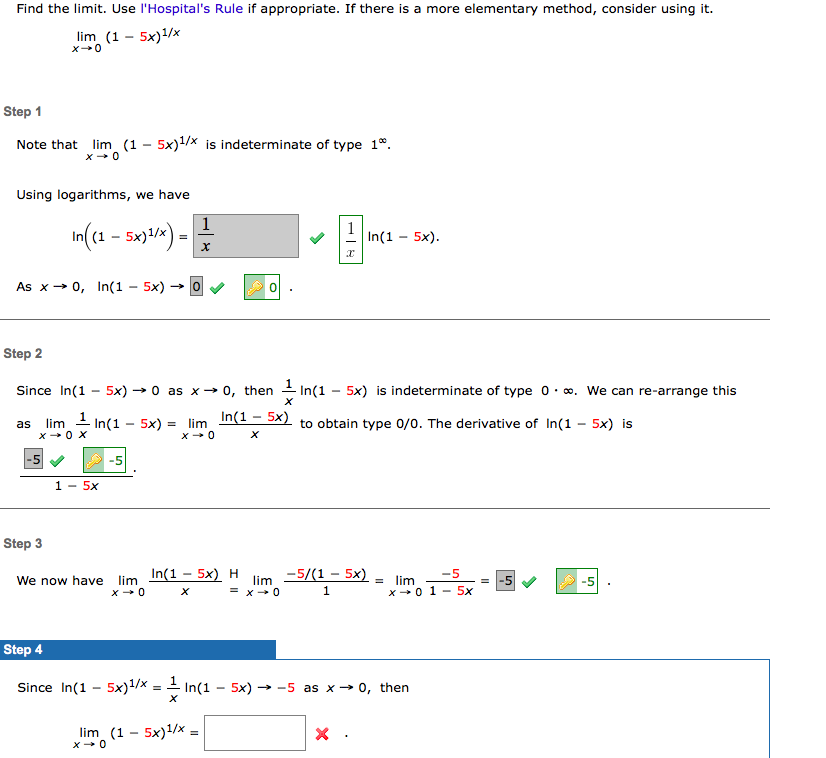 | 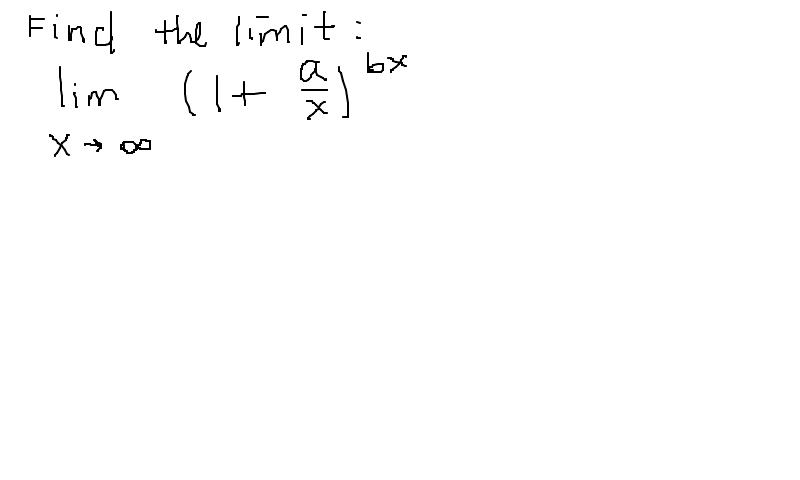 |  |
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
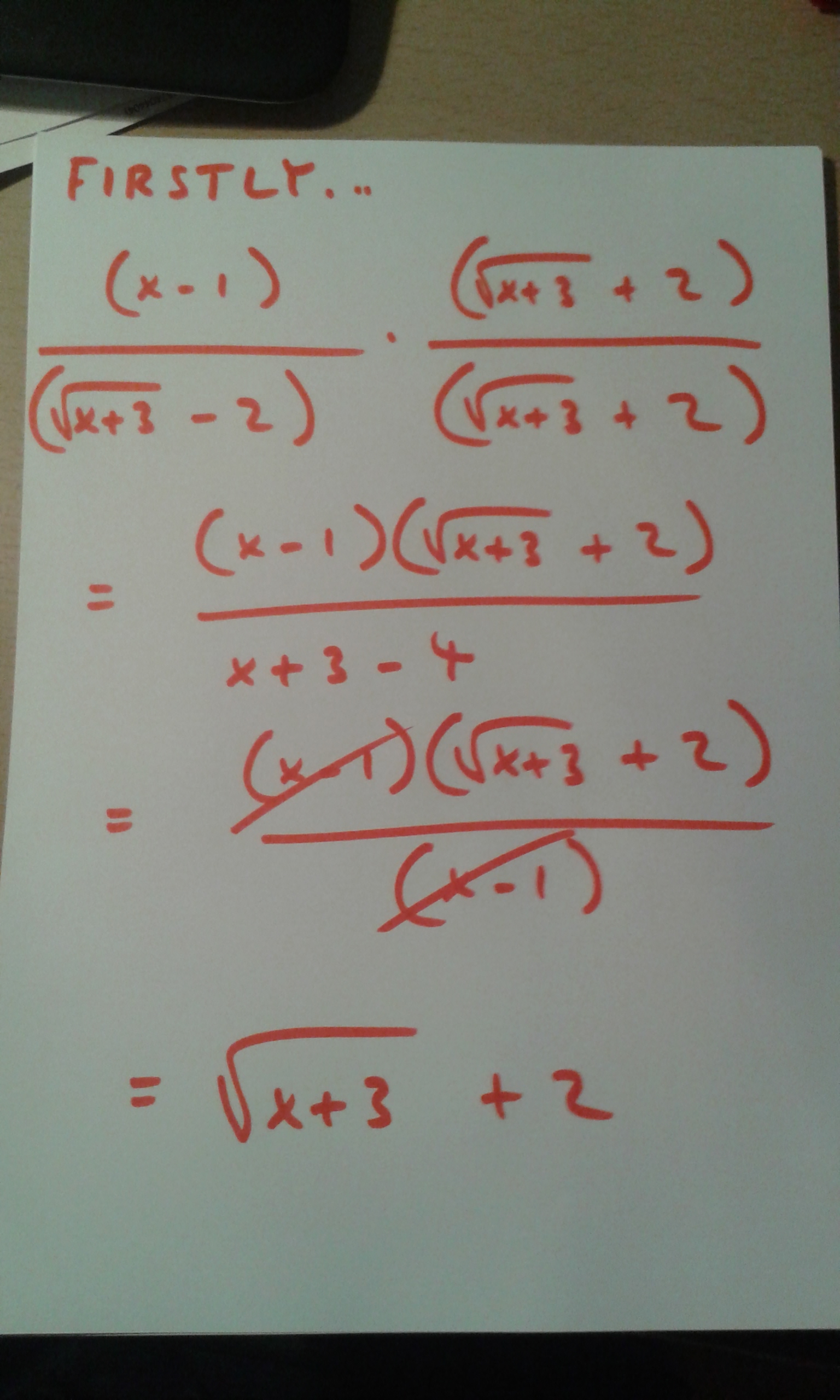 | ||
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 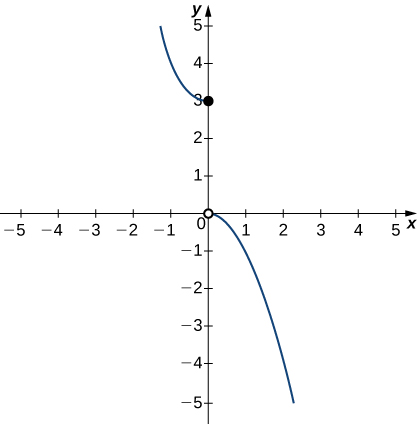 | |
 | ||
 |  |  |
 | 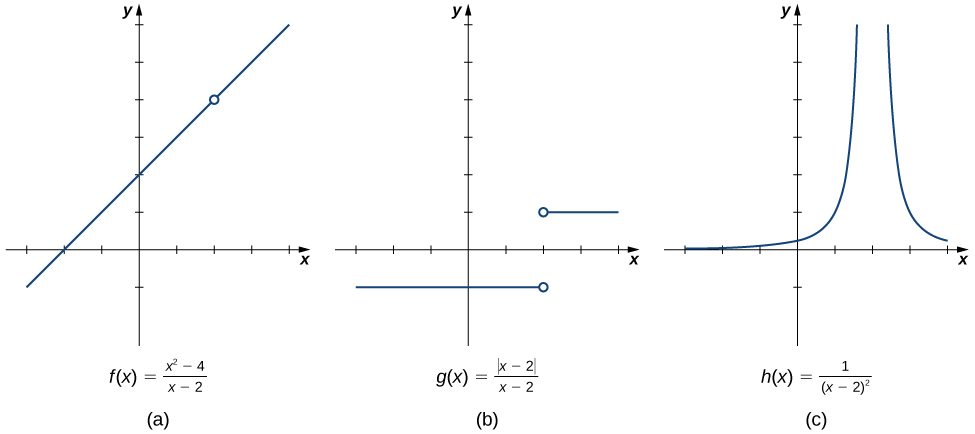 | |
「Lim x → 0 1/x^2 - cotx」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 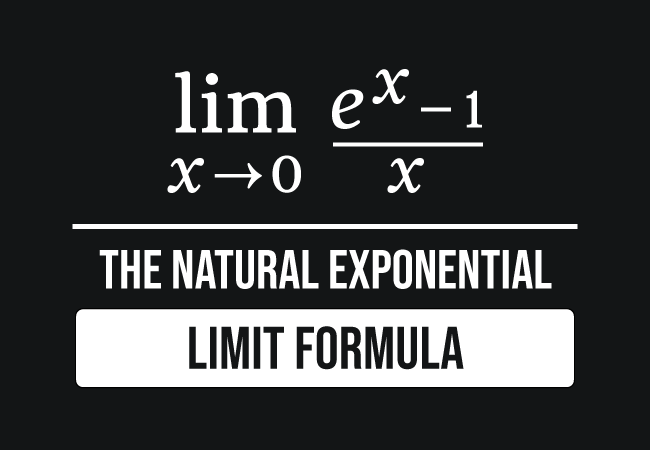 | |
 |
Answer (1 of 5) This is actually a twosided limit, because if we define f(x) = \frac{1}{x} , then \displaystyle \lim_{x \to 0^} f(x)= \infty, whereas \displaystyle \lim_{x \to 0^}f(x) = \infty The only way to find the limit value is to break it up into 0^ and 0^; $$\begin{align} \lim_{x\to 0}\frac{e^xx1}{x^2}&=\lim_{x\to 0}\frac{\frac12 x^2e^{s^*}}{x^2}\\\\ &=\frac12 \end{align}$$ as expected!
Incoming Term: lim x- 0 1/x^2, lim x- 0 (1-cosx)/x^2, lim x- 0 1-cos2x/x^2, lim x- 0 (1-cos3x)/x^2, lim x- 0 (1-cos4x)/x^2, lim x mendekati 0 1/x^2, lim x → 0 1/x^2 - cotx, lim x → 0 (1/x)^2 sinx, lim x- 0 e^(-1/x^2), lim x- 0 sin(1/x^2),
コメント
コメントを投稿